CLASS 10TH MATHS CH-6 THEOREM 6.6

Theorem 6.6 states that : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

We need to prove this theorem.

Given: Two similar triangles ABC and PQR.

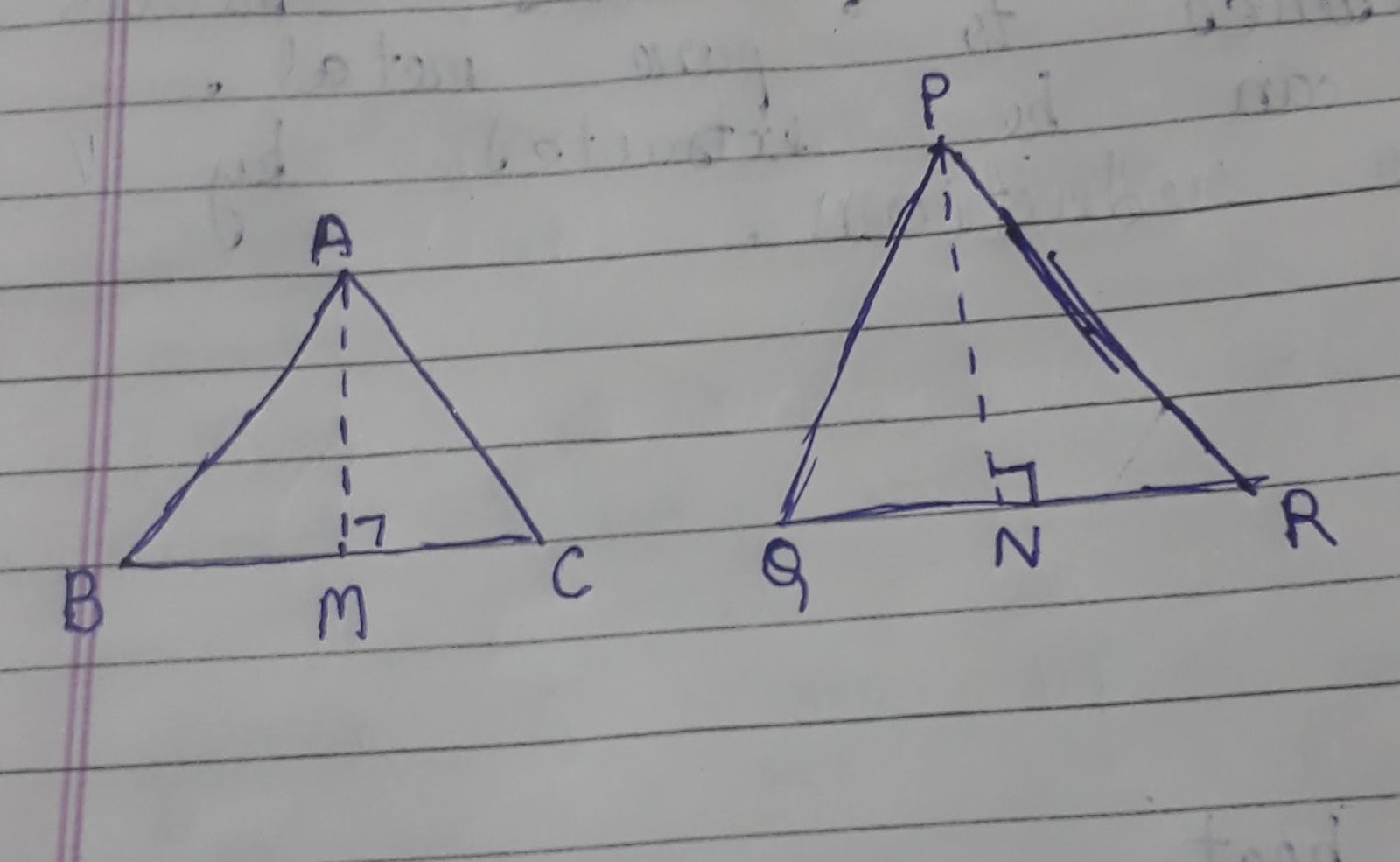
To prove: ar(ABC) = [AB]² = [BC]² 

                 ar(PQR)    [PQ]      [QR]

    = [CA]²

       [RP]

Constrution: Draw two altitudes name as AM and PN of triangles. 

Proof: Area of triangle = 1/2 × base × height 

So,  ar(ABC) = 1/2 × BC × AM

 And ar(PQR) = 1/2 × QR × PN

 

Now, the ratio of both areas,

       ar(ABC) = 1/2 × BC × AM

       ar(PQR)    1/2 × QR × PN

   

       ar(ABC) = BC × AM  (1)

       ar(PQR)    QR × PN

Now, in triangle ABM and PQN,

                √B = √Q  [ ABC ~ PQR ]

                √M = √N [ Both 90°]

         So, triangle ABM~ triangle PQN

Therefore,   AM = AB  (2)

                     PN     PQ

So,  ar[ABC] = BC × AM

       ar[PQR]     QR × PN

       ar[ABC] = BC × AB  [From (2)]

       ar[PQR]    QR    PQ

Now,  triangle ABC ~ triangle PQR  [Given]

  So,    AB = BC = CA  (3)

           PQ    QR     RP

  So,  ar[ABC] = BC × AB

         ar[PQR]    QR    PQ

         ar[ABC] = AB × AB  [From(3)]

         ar[PQR]    PQ    PQ

         ar[ABC] = [AB]²

         ar[PQR]    [PQ]

Now from (3),

    ar[ABC] = [AB]² = [BC]² = [CA]²

    ar[PQR]    [PQ]      [QR]     [RP]

Hence, Proved.

Please Subscribe to get notification for new post.